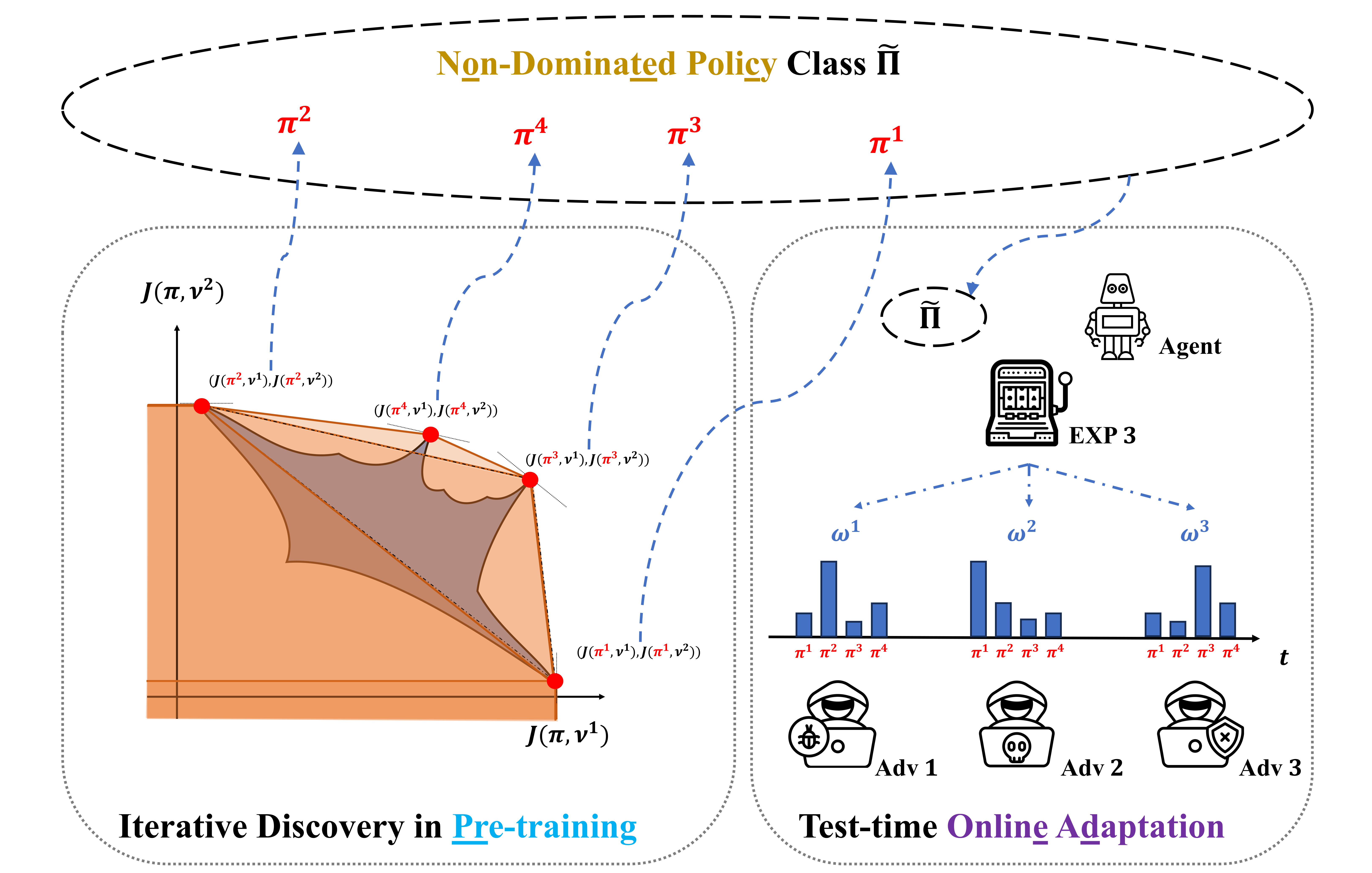

In light of the burgeoning success of reinforcement learning (RL) in diverse real-world applications, considerable focus has been directed towards ensuring RL policies are robust to adversarial attacks during test time. Current approaches largely revolve around solving a minimax problem to prepare for potential worst-case scenarios. While effective against strong attacks, these methods often compromise performance in the absence of attacks or the presence of only weak attacks. To address this, we study policy robustness under the well-accepted state-adversarial attack model, extending our focus beyond merely worst-case attacks. We first formalize this task at test time as a regret minimization problem and establish its intrinsic difficulty in achieving sublinear regret when the baseline policy is from a general continuous policy class, $\Pi$. This finding prompts us to refine the baseline policy class prior to test time, aiming for efficient adaptation within a compact, finite policy class $\widetilde{\Pi}$, which can resort to an adversarial bandit subroutine. In light of the importance of a finite and compact $\widetilde{\Pi}$, we propose a novel training-time algorithm to iteratively discover non-dominated policies, forming a near-optimal and minimal $\widetilde{\Pi}$ , thereby ensuring both robustness and test-time efficiency. Empirical validation on the Mujoco corroborates the superiority of our approach in terms of natural and robust performance, as well as adaptability to various attack scenarios.


"Is it possible to develop a comprehensive framework that enhances the performance of the victim against non-worst-case attacks, while maintaining robustness against worst-case scenarios?"
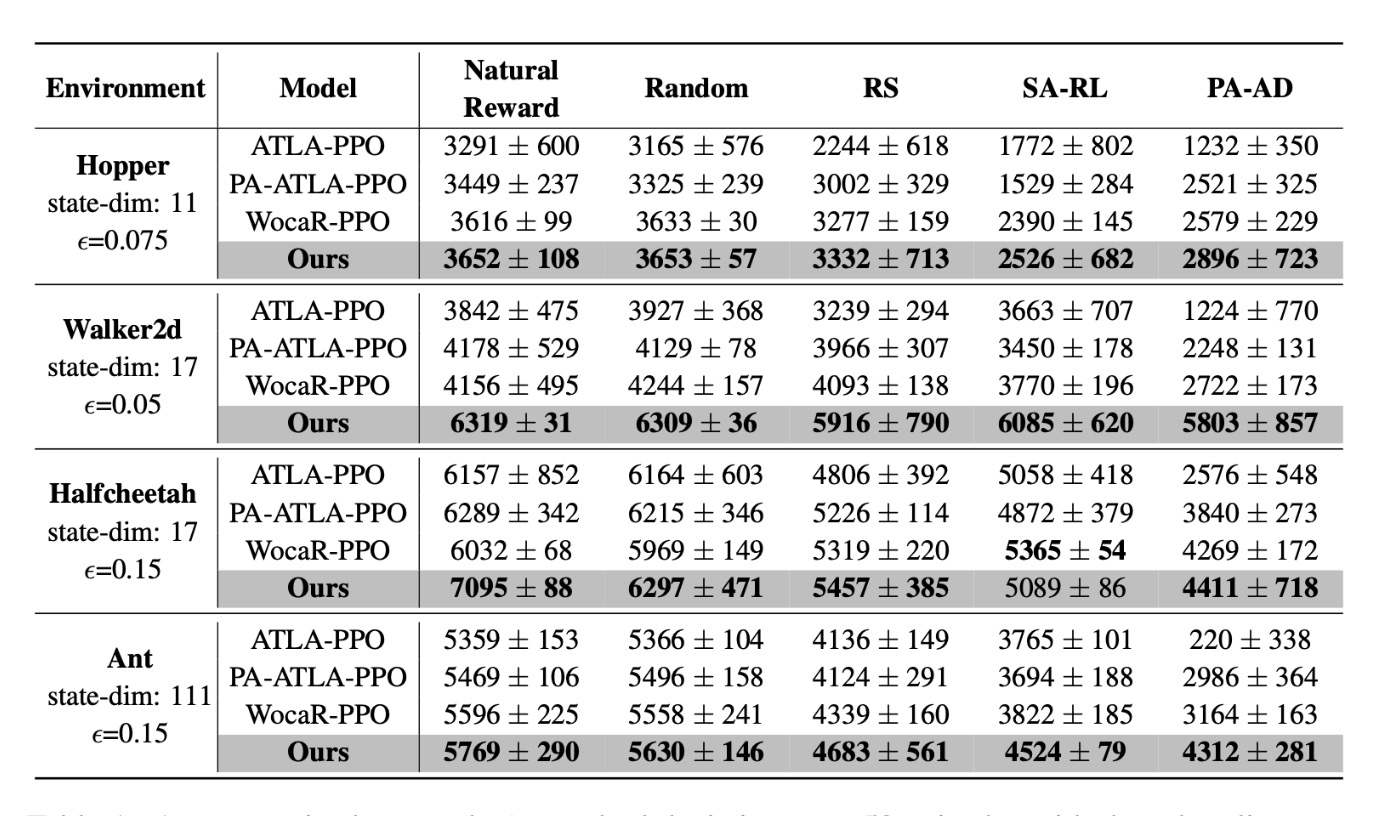
Our methods yield considerably higher natural rewards and consistently enhanced robustness against a spectrum of attacks in various Mujoco environments.
Moreover, in the scenarios where the attacker can exhibit dynamic behavior, the best policy within non-dominated policy class $\widetilde{\Pi}$ can be identified by EXP3 rapidly and reliably.

Periodical attack, $T=1000$.

Periodical attack, $T=200$.

Problistic switching attack, $p=0.4$.

Problistic switching attack, $p=0.8$.
@inproceedings{
liu2024beyond,
title={Beyond Worst-case Attacks: Robust {RL} with Adaptive Defense via Non-dominated Policies},
author={Xiangyu Liu and Chenghao Deng and Yanchao Sun and Yongyuan Liang and Furong Huang},
booktitle={The Twelfth International Conference on Learning Representations},
year={2024},
url={https://openreview.net/forum?id=DFTHW0MyiW}
}